

Computer Architecture Simulation & Visualisation

QCD Explained
QCD is a study of the physics of sub-atomic particles. It
defines the tiniest particles with which all matter is
built. According to QCD theory, the components of an atom
(Figure I), the proton and neutron, are composed of even smaller
particles called quarks and gluons. QCD theory also describes
quark and gluon interactions at various energy levels. Since
some of these particles are either very tiny or do not exist in
isolated states, a number of the theoretical predictions of QCD
cannot be verified experimentally, even using state-of-art
accelerators and colliders. The computer generated simulations
are, in several cases, the only mechanism to verify the
theoretical predictions.
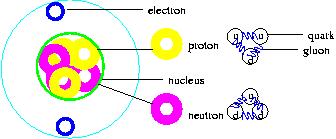
Figure I: Inside an Atom
Because of the enormous computing requirements of QCD
calculations, it is described as a 'Grand Challenge' computing
application. A grand challenge problem is one which cannot be
solved in a reasonable amount of time on currently available
parallel supercomputers. For the last three decades a number of
commercial and custom-built parallel machines have been employed
to solve QCD calculations and they have successfully produced a
number of results. The natural parallelism in QCD applications,
resulting from its lattice formulation (called lattice QCD),
makes QCD one of the first applications to be tried on early
parallel computers. Yet the QCD calculations still challenge the
power of high-end supercomputers; they continue to push the
boundaries of supercomputer architecture, QCD algorithms and
parallel software techniques.
Lattice QCD
The four-dimensional space-time lattice formulation of the QCD
theory (lattice QCD) involves a discretisation scheme; space and
time continua are discretised and represented as lattice points
(Figure II). There are two cost factors in the lattice QCD
scheme: finite boundary and lattice spacing. The lattice scheme
presents finite boundary volumes, i.e. the boundary of a lattice
which should ideally be infinite. In order to minimise the
discretisation and finite boundary errors, the lattice volume
should be as large as possible and the spacing between lattice
points should be close to zero. These two requirements are
directly responsible for the high computational requirements of
the application.
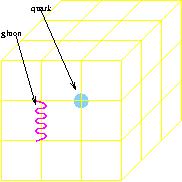
Figure II: Lattice QCD
The lattice formulation of the QCD calculation makes this
application ideally suited for implementation on a parallel
machine. This is because a regular lattice can be decomposed and
distributed evenly on a four-dimensional physical network, among
parallel processing nodes (Figure III). The communication
requirements of the QCD calculations are local i.e.
neighbouring nodes along the four space-time dimensions
communicate; global broadcast and reduction operations are rare.
The code requires intensive use of double-precision
floating-point calculations.
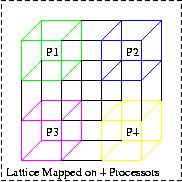
Figure III: Mapping of Lattice on to Physical Processors
Return to the QCD Computer Simulation Project

HASE Project
Institute for Computing Systems Architecture, School of Informatics,
University of Edinburgh
Last change 21/07/2004

Please contact our
webadmin with any comments or changes.
Unless explicitly stated otherwise, all material is
copyright © The University of Edinburgh.

![]()





![]()